A Simulation Study on the Generative Neural Ensemble Decoding Algorithms

Sung-Phil Kim¹ and Min-Ki Kim<sup>2

1</sup>Dept. of Brain and Cognitive Engineering, Korea University
²School of Electrical Engineering, Korea University

Abstract

Brain-computer interfaces rely on accurate decoding of cortical activity to understand intended action. Algorithms for neural decoding can be broadly categorized into two groups: direct versus generative methods. Two generative models, the population vector algorithm (PVA) and the Kalman filter (KF), have been widely used for many intracortical BCI studies, where KF generally showed superior decoding to PVA. However, little has been known for which conditions each algorithm works properly and how KF translates the ensemble information. To address these questions, we performed a simulation study and demonstrated that KF and PVA worked congruently for uniformly distributed preferred directions (PDs) whereas KF outperformed PVA for non-uniform PDs. In addition, we showed that KF decoded better than PVA for low signal-to-noise ratio (SNR) or a small ensemble size. The results suggest that KF may decode direction better than PVA with non-uniform PDs or with low SNR and small ensemble size.

1. Introduction

Recent advances in brain-computer interfaces (BCIs) promise to provide a new human-computer interface using the brain signals as well as an independent communication channel to the disabled with “locked-in” syndrome (see [1-2] for review). Thrusts of this emerging technology include neurotechnology for chronic recording, neuroscience for neural motor control and machine learning for high-dimensional spatio-temporal data processing. In particular, some machine learning algorithms play a central role in the development of BCIs mainly due to the fact that one can apply a variety of insights from the-state-of-the-art machine learning researches and it is relatively less known whether and how a technique proven in general machine learning studies works in decoding cortical activity.

The main objective of the computation algorithm is to decode cortical activity into different types of signal that can be used for controlling computer cursor, robotic devices, environment or speech [3-4]. Such algorithms for decoding may be broadly categorized into two classes: the direct model versus generative model. The class of direct models approximates a mapping between the neural space and the covariate space (e.g. kinematics space), assuming a black box model that is merely identified from observed data. The class of generative models solves an inverse problem to infer the covariate state from the observed neural data. As the generative models start from constructing an encoding model to describe how neural activity is generated from intended action, they more likely draw upon neurophysiologic findings from the analysis of the relationship between neural activity and its covariates such as movements, stimuli or other variables.

Among many generative models, the population vector algorithm (PVA) [5] and the Kalman filter [6] have been widely used for both open-loop and closed-loop BCI studies because the principles of those algorithms are well known and their computational complexities are relatively low. In particular, the PVA originated from the neurophysiologic observation of motor cortical activity in relation to arm movement direction. On contrary, it has not been well known how the Kalman filter (KF), originally developed from control theory, interprets cortical activity, especially for neuronal ensemble. A recent study by Koyoma et al. [7] has shown that, in principle, the KF decodes neural activity better than the PVA when the preferred directions (PDs) are not uniformly distributed. They also demonstrated that the smoothing effect by the system model built in the KF enhanced decoding performance. However, the results from this study did not fully address in which conditions both the PVA and the KF work congruently or differently. One obvious condition, as stated by Koyoma et al. [7], should be the uniformity of PDs. In addition to it, we also investigated other conditions including signal-to-noise ratio (SNR) as well as the ensemble size.

To study the behavior of two decoding algorithms for a different set of conditions, we simulated neural decoding by generating spike data based on Poisson model and build decoding algorithms for those synthetic data. The spike generation model was based on the linear tuning function that was a common assumption of both algorithms. The simulation study allowed us to change neuronal ensemble condition as much as possible, which is not usually possible from the recoding of real neurons by a chronic array.

2. Simulation procedure

In order to generate a spike train of a neuron, we assumed that an underlying firing rate of the neuron was linearly related to the cosine function of movement direction. The movement direction sample was generated from the 2D computer cursor movement where the user performed a randomly located target selection task. The sampling rate was 20Hz. Using this dataset, we generated a firing rate based on a linear tuning function [5]:

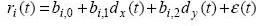
(1)

where d_x = cosθ(t) and d_y = sinθ(t). r_i(t) denotes the firing rate of a neuron i at time instant t, and b_i’s are the tuning function parameters. ε(t) is a Gaussian noise with zero mean and variance σ². Note that the length of a direction vector d, ||d||² = d_x² + d_y² = 1. A vector bi = [b_i,1 b_i,2]^T represents the preferred direction. For simplicity, we suppose ||b_i|| = 1 for all i (we can normalize the linear relation function in case ||b_i|| ≠ 1).

To generate the firing rates of N neurons, we selected the PD of each neuron such that all PDs were uniformly distributed - i.e. the angle distances between adjacent PDs were all equal to 360°/N. Then, we set b_i,1 = cosΦ_i and b_i,2 = sinΦ_i, respectively, where Φ_i was the PD of neuron i. The y-intercept, b_i,0 was determined to ensure that r_i(t) ≥ 0.

The variance of Gaussian noise (σ²) which was regarded as the noise power, was determined based on the presumed signal-to-noise power ratio (SNR). For instance, if S denotes a given SNR quantity, σ² was given by σ² = ξ / S, where ξ was the signal power estimated from the mean squared value of the sum of the first three terms in the right hand side of eq. (1). We assumed that ε(t) was white noise such that ε(t) = ε.

Next, we generated a spike train using r_i(t) obtained from eq. (1). We assumed that a spike generating process followed Poisson process: the probability that there was a spike in a short interval dt at time instant t was r_i(t)dt. We set dt = 1ms, considering the refractory period. Since r_i(t) was determined with a resolution of 50ms, we assumed that r_i(t) was constant over each 50ms period.

Once spikes were generated, we assumed that no knowledge about the true firing rate r_i(t) was available. Instead, we approximated the firing rate from the spike train using binning that has been used for most BCI studies. In a binning process, we counted spikes for a 50ms non-overlapping sliding window and deemed those spike counts to represent the firing rate. Since spikes are generated from the random process (Poisson), the true firing rate is better approximated by averaging spike count over more repetitions of spike generation process. We repeated this spike generating process K times and used the average spike count for each bin. By varying K, we examined how decoding performance was influenced by the number of repetitions to compute the average spike count.

3. Decoding algorithms

The population vector algorithm (PVA) was developed to decode movement velocity or direction from the concurrent firing activity of neuronal populations [5]. PVA has been known to be an optimal linear estimator for direction when the PDs are uniformly distributed [8]. PVA assumes a linear tuning function as depicted in eq. (1). From the observed firing rates and movement direction, PVA estimates the tuning parameters (b₀, b₁ and b₂) using least-squares (LS). Then, PVA constructs the PD vector for each neuron.

For a new neuronal ensemble data that is not used for parameter estimation, PVA decodes direction using the weighted sum of PDs:

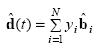
(2)

where the weight y_i is the normalized version of the observed firing rate of neuron i.

The Kalman filter (KF) is a special form of Bayesian recursive estimator where it is assumed that the observation model and the system model are linear Gaussian [6]. The major difference of KF and PVA is that KF builds the system model that describes how the movement evolves in time. The system model smoothes the decoded kinematic trajectory [7] as well as incorporates intrinsic dynamics of the arm movement if constructed properly.

Similar to PVA, KF builds an encoding model using eq. (1). While PVA builds N individual encoding models for each neuron, KF builds only one encoding model (or called the observation model in KF literatures) that maps the 2D direction space to the N-dim neural space.

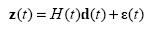
(3)

H(t) is the matrix of the linear tuning function, which is estimated from the training data by LS. We also estimate the covariance matrix of ε(t) where ε(t) is assumed to be a multivariate Gaussian random vector with zero mean and covariance Q(t). We assumed that H and Q are time invariant.

The system model of KF is constructed in the same way as the observation model, assuming that it follows Markov process and is a linear model:

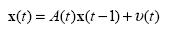
(4)

Again, A(t) and the covariance of υ(t) are estimated using LS and assumed to be time-invariant.

Once the model parameters are estimated from training data, KF decodes movement kinematics using a closed-form solution with two steps: prediction of the kinematics at time t from t-1 using the system model and update of the kinematics estimate using the difference between the predicted and the newly observed neural data (see [6] for details). While KF can be used to decode any or all of kinematic variables such as position, velocity and acceleration [6], PVA has been only shown to work for decoding velocity or its directional component [5]. Hence, we considered decoding movement direction using PVA and KF in this study for unbiased comparison.

4. Results

In simulation, we generated 3-min data using the movement direction samples recorded from the computer cursor movement during a random pursuit task and divided it into a 2.5 min training set and a 0.5-min testing set. Using the same data, we trained and tested both PVA and KF. Direction decoding performance was evaluated by measuring the mean angular difference (AD) between the true and the estimated direction vectors for the testing set.

First, we investigated how decoding performance varied with SNR how much noise was added to firing rate generation as in eq. (1). The number of repetition to generate spikes to obtain the mean spike count was set to 100. Forty two neurons were generated. The PDs of these neurons were uniformly selected between 0 to 360 degrees. As expected, AD decreased as SNR increased (i.e. less noise was added). Figure 1 shows that AD exponentially decreased as SNR (in dB) increased. PVA and KF showed almost identical decoding accuracy for high SNR whereas KF exhibited more accurate decoding than PVA for low SNR.

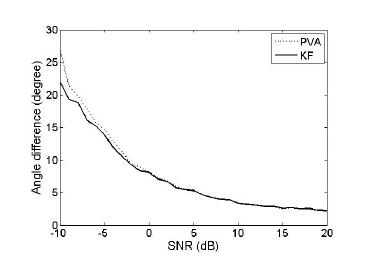
Figure 1. Angle difference versus SNR. Angle difference between true and estimated movement direction decoded by either PVA (dotted line) or KF (solid line) was evaluated for the range of signal-to-noise ratio (SNR).

Second, we investigated how decoding performance varied with the number of neurons. The PD distribution remained uniform no matter how many neurons were generated. SNR was fixed to be 3dB. Figure 2 shows that AD exponentially decreased as more neurons were used for direction decoding (i.e. neuronal ensemble size increased). Again, PVA and KF showed similar accuracy for a large number of neurons whereas KF slightly performed better than PVA when only a small number of neurons were used.

Third, we empirically examined how many repetitions of the Poisson-based spike generating process needed to obtain the mean spike count which could represent an underlying firing rate sufficiently well. As the underlying firing rate used in this study was also generated from noisy function of direction, we evaluated decoding accuracy as a function of the number of repetitions, instead of directly evaluating how close the mean spike count was to the original firing rate. We found that AD converged to a constant level with around 93 repetitions (see Figure 3).

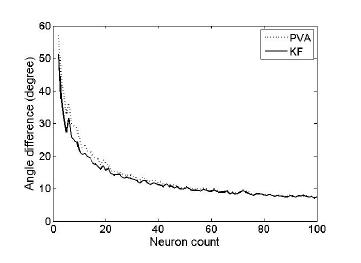
Figure 2. Angle difference versus the number of neurons. Angle difference was evaluated as a function of the number of neurons used for decoding: with either PVA (dotted) or KF (solid).

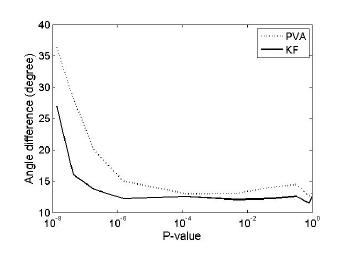
Figure 3. Angle difference versus the number of repetitions. Angle difference was evaluated as a function of the number of repetitions.

Finally, we investigated the case of non-uniform PD distribution. Uniformity of PDs was quantified by the p-value of the Rayleigh test (used for circular uniformity test). A smaller p value indicates a less uniform circular distribution. Comparison of decoding accuracy presented in Figure 4 between PVA and KF demonstrated that KF outperformed PVA when the PDs of neurons were not uniformly distributed. This results supports previous suggestions that PVA worked optimally only for uniformly distributed PDs [7-8].

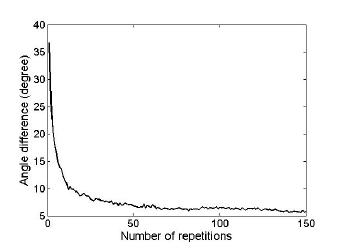
Figure 4. Angle difference versus the degree of uniformity. Angle difference was described with a range of degrees of uniformity using PVA (dotted) or KF (solid).

5. Conclusion

In this simulation study, we demonstrated that the population vector algorithm was suboptimal for movement direction decoding when the PDs of a given neuronal ensemble were not uniformly distributed. This supports the previous findings claiming similar observations [7]. However, we drew this statement with a statistically designed simulation by controlling uniformity in a systematic way. We also investigated the effect of other parameters on decoding accuracy in our simulation, including the amount of noise added to firing rate signals or the number of neurons. It showed that the Kalman filter and the population vector showed similar performance for “good” conditions with high SNR, many neurons and uniform PDs, while the Kalman filter worked better otherwise. We expect that this study contributes to better understanding of generative decoding algorithms and how to choose one for given assumptions on the data. As both KF and PVA would remain as a primary decoding method for closed-loop BCI systems, this study may provide useful information for designing an optimal BCI.

References

[1] J. P. Donoghue. Bridging the brain to the world. Neuron, 60:511–521, 2008.

[2] B. Z. Allison, E.W. Wolpaw and J. R. Wolpaw. Brain-computer interface systems: progress and prospects. Expert Review of Medical Devices 4(4): 463-474, 2007.

[3] A. B. Schwartz, D.M. Taylor and S. I. Helms Tillery. Extraction algorithms for cortical control of arm prosthetics. Curr. Opin.Neurobiology, 11: 701-707, 2001.

[4] S. P. Kim, J. C. Sanchez, Y. Rao, D. Erdogmus, J. M. Carmena, M. A. Lebedev, M.A.L. Nicolelis and J. P. Principe. A comparison of optimal MIMO linear and nonlinear models for brain-machine interfaces. J Neural Eng., 3: 145-161, 2006.

[5] D. W. Moran and A. B. Schwartz. Motor cortical representation of speed and direction during reaching. J Neurophysiol., 82: 2676-2692, 1999.

[6] W. Wu, Y. Gao, E. Bienenstock, J. P. Donoghue and M. J. Black. Bayesian population decoding of motor cortical activity using a Kalman filter. Neural Computation, 18(1): 80-118, 2006.

[7] S. Koyoma, S. M. Chase, A. S. Whitford, M. Velliste, A. B. Schwartz and R. E. Kass. Comparison of brain-computer interface decoding algorithms in open-loop and closed-loop control. J Comp. Neurosci., online, 2009 .

[8] E. Salinas and L. F. Abbott. Vector reconstruction from firing rates. J Comp. Neurosci., 1: 89-107, 1994.

About the Authors

Sung-Phil Kim earns his M.S. and Ph.D. degrees in Electrical and Computer Engineering from University of Florida and B.S. degree in Nuclear Engineering from Seoul National University. He was working in the BrainGate research team at Brown University as a postdoctoral Research Associate. He is currently an Assistant Professor at Department of Brain and Cognitive Engineering, Korea University, Seoul, South Korea. His research focuses include brain-computer interfaces (BCI), EEG pattern analysis and synchrony, neural population codes, and statistical signal processing.

Min-Ki Kim is a M.S. candidate in Electrical Engineering from Korea University, Seoul, Korea. He earned the B.S. degree in Electrical Engineering from Wonkwang University, Korea. He is currently working in the intelligent system research laboratory at Korea University. His primary researches include brain-computer interface (BCI), neural decoding algorithms, and EEG signal processing.