Hybrid Nature-Inspired Computation Methods for Optimization
Department of Electrical Engineering
Helsinki University of Technology
Otakaari 5 A, FI-02150 Espoo, Finland
Tel.: +358 9 47024965, Fax: +358 9 47022432
E-mails:
Abstract
The past decade has witnessed the overwhelming successes of hybrid Nature-Inspired Computation (NIC) methods, which can effectively combat with the individual drawbacks while benefiting from each other's strengths. This paper gives a brief overview on the standalone NIC methods as well as their hybridizations in the field of optimization.
1. Introduction
The development of modern science and technology requires flexible, reliable problem-solving methods. The Nature-Inspired Computation (NIC) methods represent such an emerging computing paradigm that draw their metaphorical inspiration from diverse natural sources, including the operation of biological neurons, evolution processes, and natural immune responses [1]. Many engineering optimization problems are indeed complex and have builtin uncertainties as well. It is well known that conventional optimization approaches usually require some prior information beforehand, which is often either difficult to acquire or even unavailable [2]. During recent years, the NIC methods have gained considerable attention from different communities [3]. Compared with the traditional optimization schemes, the NIC methods are more suitable candidates for dealing with the demanding problems faced by industry, and can thus offer us robust, competitive solutions. As a matter of fact, for the optimization applications in such fields as pattern recognition, self identity, data analysis, and machine learning, the NIC methods are capable of outperforming the classical techniques by providing better and more flexible solution choices. In the following sections, we first present a short introduction to several most widely applied NIC methods. A concise discussion on the hybrid NIC methods for optimization is next given. Finally, some conclusions and remarks are drawn.
2. Nature-inspired computation methods
The NIC methods refer to as those algorithms derived by mimicking natural phenomena and biological models. For instance, the Clonal Selection Algorithm (CSA) draws its inspiration from natural immune systems, which can prevent the human body from invasion by disease-causing pathogens [4]. The collective behaviors of the foraging of ants, mound construction of termites, nest-building of wasps, and web-weaving of spiders have been studied and have inspired the so-called Swarm Intelligence (SI) algorithms [5]. The NIC methodologies, such as the CSA, Particle Swarm Optimization (PSO) [6], Ant Colony Optimization (ACO) [7], Simulated Annealing (SA) [8], Harmony Search (HS) [9], Differential Evolution (DE) [10], and Mind Evolution Computing (MEC) [11], are emerging types of Soft Computing (SC) or Computational Intelligence (CI) methods [12]. These typical algorithms have two common characteristics in mimicking natural phenomena:
- Inspiration drawn from nature,
- Modeling of natural processes.
The NIC techniques usually have a general flowchart, as shown in Fig. 1 [13]. Firstly, an initial collection of candidate solutions are randomly generated (Initialize). Next, new members are produced by making changes to the selected candidates, and they are then evaluated (Operate). The changes here may involve merging two or more existing members together or introducing random variations to the current candidates. Lastly, those solutions that are outdated are replaced with the improved ones (Renew). Such a competitive strategy results in appropriate candidates for generating new solutions in the next generation. Hence, the key ideas underlying most NIC approaches are candidate generation, evaluation, selection, and update.
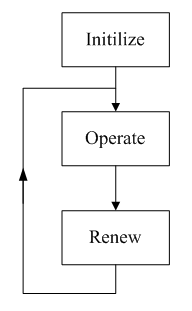
Fig. 1. General flowchart of NIC algorithms.
We can observe that the above NIC methodologies share many obvious similarities, e.g., adaptation, learning, and evolution. On the other hand, they also have some distinct differences, and each has its own advantages and drawbacks [14]. Table 1 summarizes the advantages and shortcomings of these NIC algorithms. For example, the CSA and ACO can deal with multi-modal and dynamical optimization problems, respectively [15].
| NIC algorithm | Advantages | Disadvantages |
| ACO | Pheromone-based elitism | Over-similarity |
| CSA | Diversity | Slow convergence speed |
| DE | Effective search | High computational effort |
| HS | Algorithm simplicity | Outdated information |
| MEC | Anti-premature | Time-consuming |
| PSO | Information sharing | Premature |
| SA | Robustness | Long computation time |
Although they have attracted considerable research attention, due to their outstanding performances compared to the conventional optimization solutions, the standalone NIC methods are still not efficient enough at handling uncertainty and imprecision in practice. Additionally, practicing engineers often face the difficulty of choosing the most suitable NIC methods to meet particular engineering requirements. Therefore, numerous hybrid optimization schemes based on the fusion of these NIC algorithms have been investigated, which can overcome the individual shortcomings.
3. Hybrid nature-inspired computation methods for optimization
As we know that all the NIC methods have their strengths and drawbacks, since they are based on only certain phenomena in nature. Among them, the PSO is inspired by the flocking of birds, fish schooling, and the ACO foraging behaviors of ants. However, if used separately, the weaknesses of these algorithms may hinder their wider employment in attacking challenging optimization problems. That is to say, the NIC methods are complementary rather than competitive. It is generally advantageous to apply them in combination instead of individually. For example, the harmful particle clustering of the original PSO method can be avoided by introducing operations from other NIC algorithms so as to randomly disturb the trend of solution centralization. The performance of the regular HS method might be significantly enhanced, if the Harmony Memory (HM) members are fine-tuned on the basis of the CSA. Thus, utilizing the advantages of various NIC techniques while avoiding their drawbacks promotes the advances in the hybridization research.
During the past decade, hybridization of the NIC algorithms has gained significant popularity, thus helping to overcome the individual weaknesses while benefiting from each other's strengths. Indeed, fusion of the NIC methods, e.g., combination of the ACO and CSA, can offer us competitive solutions with improved performances for numerous optimization problems. The inspiration and fusion of some representative NIC techniques are shown in Fig. 2.
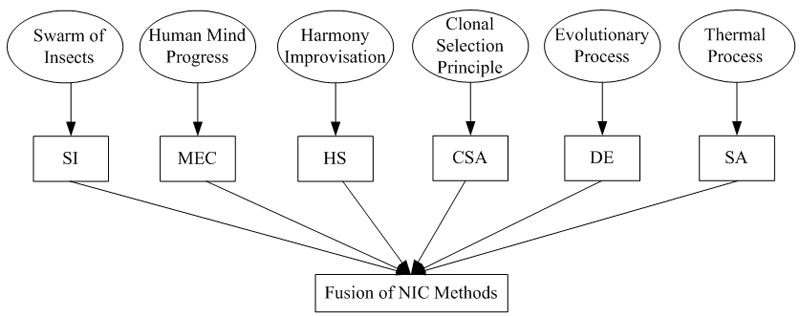
Fig. 2. Inspiration and fusion of typical NIC methods.
The aforementioned hybridization strategies have been developed with the aim of coping with specific types of optimization problems. For instance, the ACO, a powerful NIC technique, has been merged with the CSA for solving the optimization problems under dynamic environments [15]. Fusion of the SA and CSA can result in a hybrid CSA with an improved global search capability for nonlinear problems [16]. In a word, the motivation for hybridization is to improve the convergence acceleration, robustness, and reliability.
In general, the hybrid NIC methods can be classified into different categories according to the measures used, e.g., motivation for hybridization and architecture of hybridization. As an illustrative example, they are divided into three categories according to the nature of their architectures.
- Preprocessors and postprocessors: This is the most popular hybridization type, in which the NIC techniques are applied sequentially, i.e., data/information generated by Algorithm A (preprocessor) can be fine-tuned by Algorithm B (postprocessor). For example, in [17], the CSA is employed to improve the fitness of the solution candidates in the HM. In other words, all the members of the HM are regarded as the individual antibodies (Abs), and they can evolve in the population of the CSA.
- Cooperators: It illustrates such a hybrid NIC system, in which the two algorithms involved simultaneously adjust each other. Common information is exchanged and shared between the algorithms during the search process. For example, the evolutionary computation method and fuzzy inference technique are fused together in a hybrid evolutionary-fuzzy system for nonlinear function approximation. These two approaches can optimize, fine-tune, and control the parameters of each other [18].
- Embedded: The hybrid NIC methods belonging to this class are characterized by their architectures, in which Algorithm B is embedded inside Algorithm A. A typical scheme is to combine the local search and global search from different NIC techniques together in order to improve the overall convergence of the hybridization. For example, in [19], the dissimilation and similartaxis operations from the CSA are incorporated in the MEC, which aim at accelerating the global and local optimal search, respectively.
The hybridization can lead to the following benefits:
- Improvement of convergence performance,
- Enhanced solution quantity and quality,
- Creation of compact, reconfigurable systems.
Actually, a careful and comprehensive analysis of the classification of the hybridization would help us not only gain a deep understanding of the NIC methods but also choose the best combinations for targeted optimization problems. To summarize, studying the hybridization of these NIC methods allows us to overcome the shortcomings of individual algorithms while at the same time retaining their individual advantages.
4. CSA-DE: an example of hybrid NIC methods
In this section, we will discuss an interesting example of the hybrid NIC methods: CSA-DE, which merges the CSA and DE together. The CSA is based on the Clonal Selection Principle (CSP) that explains how an immune response is mounted when a non-self antigenic pattern is recognized by the B cells. Unfortunately, empirical study has shown that the CSA usually suffers from a slow search speed. The DE method is a simple but universal numerical optimizer. All the individuals in the DE are updated by an amount of the difference between two randomly chosen ones. The DE has the distinguishing advantages of computation simplicity as well as convergence efficiency. In [20], inspired by the fusion of the CSA and DE, we propose a hybrid NIC algorithm: CSA-DE.
In the CSA, the cloning and mutation of the Abs have the important role of ‘blind’ search because of their random characteristics. However, such a blind search is not always sufficiently efficient for dealing with the demanding complexity in real-world optimization problems. Combining these two operations and gradient-based local search strategies can indeed improve the convergence of the regular CSA. But, the gradient information is often difficult if not impossible to obtain in practice. The CSA-DE, a combination of the CSA and DE, is developed on the basis of the estimated gradient directions from the DE. The principle of our CSA-DE is that all the clones of the CSA Abs are updated and optimized using the DE, as illustrated in Fig. 3. Suppose an Ab in the CSA has been cloned and mutated into N clones, Ab1,Ab2,Ab3...AbN. These Ab clones can be alternatively considered as the individuals in a population of the DE. For instance, Ab1 is updated to Ab'1 after a given number of the DE iterations. Hence, the resulting Ab'1,Ab'2,Ab'3...Ab'N are expected to occupy their higher affinities than that of Ab1,Ab2,Ab3...AbN, and they will continue the normal CSA evolution thereafter.

Fig. 3. DE-based optimization of Ab clones in CSA-DE.
The proposed CSA-DE has two remarkable features. Firstly, in the original CSA, the Ab clones are generally independent, and have no interaction with each other. In our CSA-DE, aided by the DE, they make full use of the information sharing and exchange among themselves, and work collectively to improve their affinities. This approach can efficiently prevent the harmful prematurity of the CSA. Secondly, to build the CSA-DE, we do not need to make any major modification on the regular CSA. The DE is embedded into the CSA as an ‘internal’ fine-tuning procedure. Therefore, the implementation of our CSA-DE is fairly easy and straightforward.
Five nonlinear function optimization benchmarks have been employed to explore the efficiency of this CSA-DE. It is further used in the optimal training of the Cascade-Correlation (C-C) neural network, which is an adaptive self-growing feedforward neural network [21]. Comparison simulations have demonstrated that the CSA-DE can outperform the original CSA with regard to the convergence speed.
5. Conclusions
This paper first gives a brief introduction to some important NIC algorithms for optimization. The principles of typical hybrid NIC methods are next explained. These hybrid NIC approaches can yield superior optimization performances over the existing schemes with regard to search efficiency, convergence speed, as well as quantity and quality of the optimal solutions obtained. Although the hybridization of the NIC optimization methods has been proven to be superior to the standalone techniques in dealing with certain practical problems, we should emphasize that the ‘No Free Lunch’ theorem is a fundamental barrier to the exaggerated claims of the power and efficiency of any specific optimization algorithm [22]. However, a promising way to handle the negative implication of the ‘No Free Lunch’ theorem is to restrict the applications of a given hybrid NIC optimization algorithm to only a particular type of tasks.
6. References
| [1] | L. N. de Castro, "Fundamentals of natural computing: An overview," Physics of Life Reviews, vol. 4, no. 1, pp. 1-36, 2007. |
| [2] | K. Lange, "Optimization," New York, NJ: Springer-Verlag, 2004. |
| [3] | L. N. de Castro, "Fundamentals of Natural Computing: Basic Concepts, Algorithms, and Applications," Boca Raton, FL: Chapman & Hall/CRC, 2006. |
| [4] | L. N. de Castro and J. Timmis, "Artificial Immune Systems: A New Computational Intelligence Approach," London, UK: Springer-Verlag, 2002. |
| [5] | A. P. Engelbrecht, "Fundamentals of Computational Swarm Intelligence," West Sussex, England: John Wiley & Sons Ltd, 2005. |
| [6] | R. Eberhart and Y. Shi, "Particle swarm optimization: Developments, applications and resources," in Proceedings of the IEEE Congress on Evolutionary Computation, Seoul, Korea, May 2001, pp. 81-86. |
| [7] | M. Dorigo, M. Birattari, and T. Stutzle, "Ant colony optimization," IEEE Compu-tational Intelligence Magazine, vol. 1, no. 4, pp. 28-39, 2006. |
| [8] | R. H. J. M. Otten and L. P. P. P. van Ginneken, "The Annealing Algorithm," Boston, MA: Kluwer, 1989. |
| [9] | K. S. Lee and Z. W. Geem, "A new meta-heuristic algorithm for continuous engi-neering optimization: harmony search theory and practice," Computer Methods in Applied Mechanics and Engineering, vol. 194, no. 36-38, pp. 3902-3922, 2005. |
| [10] | K. Price, R. Storn, and J. Lampinen, "Differential Evolution ¾ A Practical Ap-proach to Global Optimization," Secaucus, NJ: Springer-Verlag, 2005. |
| [11] | C. Sun, Y. Sun, and W. Wang, "A survey of MEC: 1998-2001," in Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Hammamet, Tunisia, October 2003, pp. 648-656. |
| [12] | A. P. Engelbrecht, Computational Intelligence: An Introduction," West Sussex, England: John Wiley & Sons Ltd, 2007. |
| [13] | D. W. Corne, M. Dorigo, and F. Glover (Eds.), New Ideas in Optimization," Berk-shire, UK: McGraw-Hill, 1999. |
| [14] | A. Abraham and C. Grosan (Eds.), Engineering Evolutionary Intelligent Systems," Berlin, Germany: Springer-Verlag, 2008. |
| [15] | X. Wang, X. Z. Gao, and S. J. Ovaska, "A hybrid optimization algorithm based on ant colony and immune principles," International Journal of Computer Science and Applications, vol. 4, no. 3, pp. 30-44, 2007. |
| [16] | X. Wang, X. Z. Gao, and S. J. Ovaska, "A hybrid artificial immune optimization method," International Journal of Computational Intelligence Systems, vol. 2, no. 3, pp. 249-256, 2009. |
| [17] | X. Wang, X. Z. Gao, and S. J. Ovaska, "Fusion of clonal selection algorithm and harmony search method in optimization of fuzzy classification systems," International Journal of Bio-Inspired Computation, vol. 1, no. 1-2, pp. 80-88, 2009. |
| [18] | F. Herrera, M. Lozano, J. L. Verdegay, "Tackling fuzzy genetic algorithms," Ge-netic Algorithms in Engineering and Computer Science. G. Winter, J. Periaux, M. Ga-lan, and P. Cuesta (Eds.), New York, NJ: John Wiley & Sons Ltd, 1995. |
| [19] | X. Wang, X. Z. Gao, and S. J. Ovaska, "A hybrid optimization algorithm in pow-er filter design," in Proceedings of the 31st Annual Conference of the IEEE Industrial Electronics Society, Raleigh, NC, November 2005, pp. 1335-1340. |
| [20] | X. Z. Gao, X. Wang, and S. J. Ovaska, "Fusion of clonal selection algorithm and differential evolution method in training cascade-correlation neural network," Neuro-computing, vol. 72, no. 10-12, pp. 2483-2490, 2009. |
| [21] | S. E. Fahlman and C. Lebiere, "The cascade-correlation learning architecture," Technical Report, CMU-CS-90-100, Pittsburgh, PA: Carnegie Mellon University, 1991. |
| [22] | D. H. Wolpert and W. G. Macready, "No free lunch theorems for optimization," IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67-82, April 1997. |
About the Author
 Xiaolei Wang received her D.Sc. (Tech.) degree from the Helsinki University of Technol¬ogy, Finland in 2009. She is now working as a postdoc research fellow at the same university. Her research interests are nature-inspired computing methods for data mining and optimization.
Xiaolei Wang received her D.Sc. (Tech.) degree from the Helsinki University of Technol¬ogy, Finland in 2009. She is now working as a postdoc research fellow at the same university. Her research interests are nature-inspired computing methods for data mining and optimization.
 Xiao-Zhi Gao received his D.Sc. (Tech.) degree from the Helsinki University of Technol¬ogy, Finland in 1999. Since January 2004, he has been working as a Docent at the same university. He has published more than 180 technical papers on refereed journals and international conferences. His current research interests are neural networks, fuzzy logic, and evolutionary intelligence.
Xiao-Zhi Gao received his D.Sc. (Tech.) degree from the Helsinki University of Technol¬ogy, Finland in 1999. Since January 2004, he has been working as a Docent at the same university. He has published more than 180 technical papers on refereed journals and international conferences. His current research interests are neural networks, fuzzy logic, and evolutionary intelligence.
 Seppo J. Ovaska received his D.Sc. (Tech.) degree from the Tampere University of Technology, Finland, in 1989. He is currently a Professor at the Helsinki University of Technology, Finland. His research interests are in computationally intelligent hybrid systems, evolutionary computation, artificial life, and artificial immune systems. He has published more than 80 journal articles and more than 140 conference publications.
Seppo J. Ovaska received his D.Sc. (Tech.) degree from the Tampere University of Technology, Finland, in 1989. He is currently a Professor at the Helsinki University of Technology, Finland. His research interests are in computationally intelligent hybrid systems, evolutionary computation, artificial life, and artificial immune systems. He has published more than 80 journal articles and more than 140 conference publications.


