June 2009
Issue #27
Home
Fuzzy Logic System Research

Introduction to Interval Type-2 Fuzzy Logic Controllers -
Towards Better Uncertainty Handling in Real World Applications

Hani Hagras and Christian Wagner
The Computational Intelligence Centre
School of Computer Science and Electronic Engineering
University of Essex
Wivenhoe Park, Colchester, CO4 3SQ
United Kingdom

Abstract

Most real world applications face high levels of uncertainties that can affect the operations of such applications. Hence, there is a need to develop different approaches that can handle the available uncertainties and reduce their effects on the given application. To date, Type-1 Fuzzy Logic Controllers (FLCs) have been applied with great success to many different real world applications. The traditional type-1 FLC which uses crisp type-1 fuzzy sets cannot handle high levels of uncertainties appropriately. Nevertheless it has been shown that a type-2 FLC using type-2 fuzzy sets can handle such uncertainties better and thus produce a better performance. As such, type-2 FLCs are considered to have the potential to overcome the limitations of type-1 FLCs and produce a new generation of fuzzy controllers with improved performance for many applications which require handling high levels of uncertainty. This paper will briefly introduce the interval type-2 FLC and its benefits. We will also present briefly some of the type-2 FLC real world applications.

1. Introduction

Before the 20th century, science was considered to be devoid of uncertainty. In fact, it was the purpose of scientific progress to formulate the real world using rules, concepts and paradigms which could be proved with absolute certainty and as such to eliminate all uncertainty. The scientific view at the time is summarized by Scottish physicist and mathematician William Thomson (better known as Lord Kelvin) in his statement made at the end of the 19th century [Kelvin 1891]: “In physical science a first essential step in the direction of learning any subject is to find principles of numerical reckoning and practicable methods for measuring some quality connected with it. I often say that when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind".

It was only at the end of the 19th century that the dogma of absolute certainty in science began to show initial weaknesses. In 1871, Austrian physicist Ludwig Boltzmann introduced what became known as statistical thermodynamics, a theory developed initially to study the motions of gas molecules in a closed space. This was soon followed by the establishment of a new field of physics which applied the same statistical reasoning in a mechanical context: statistical mechanics. The main difference between these new and traditional science disciplines was the use of statistics (and probability theory) in order to avoid the problems of Newtonian mechanics which were not suitable for the complex systems (at this microscopic level) at hand. As Klir notes in [Klir 2006]: “When statistical mechanics was accepted, by the scientific community as a legitimate area of science at the beginning of the 20th century, the negative attitude toward uncertainty was for the first time revised. Uncertainty became recognized as useful, or even essential, in certain scientific enquiries.”

The introduction of Einstein’s special theory of relativity and later general theory of relativity further challenged areas of science traditionally considered as certain such as the Galilean transformations of classical mechanics. In 1926 Werner Heisenberg formulated the principle of uncertainty, “a principle of quantum mechanics implying that certain pairs of observables (e.g. the momentum and position of a particle, the energy and lifetime of a quantum level) cannot both be precisely and simultaneously known, and that as one of any pair is more exactly defined, the other becomes more uncertain”.

While uncertainty became firmly established as a part of science, it was taken for granted that all occurrences of uncertainty could be handled by probability theory [Klir 2006]. During the second half of the 20th century, it quickly became apparent that fundamentally new mathematical models and methods were required as the existing frameworks (i.e. classical - no uncertainty or uncertainty modelled through probability) could not address the uncertainty as it was present in the huge class of real world problems.

Fuzzy Logic is considered to be one of those methods suitable for modelling uncertainty. Since its appearance in the 1960s, Fuzzy Logic has continuously grown in terms of popularity and number of applications. Nevertheless, one major criticism of fuzzy logic theory which was proposed early on mainly by researchers with a statistics background is the argument that Fuzzy Logic can be subsumed by probability theory. This claim has been addressed in a variety of sources, in particular, a detailed revision and comparison of the mentioned fields of probability theory, possibility theory and fuzzy logic has been conducted in [Dubois 1993]. The fundamental goal of probability theory is the definition of the likelihood of occurrence of an event or condition. Consider the example of a scuba tank containing breathable air for 1 hour of diving when filled. If we say “There is a 50% chance that the tank was filled during the last maintenance”, it means that the likelihood of the tank being empty or filled is equal. Continuing the example, if a diver was to be diving using this scuba tank, there is a 50% chance that the scuba tank is empty, thus resulting in a serious risk for the diver.

Fuzzy Logic on the other hand does not focus on the likelihood of occurrence of an event or condition, but on the degree of truth of this event or condition. Revisiting the Scuba Tank example, if a degree of truth is 50%, i.e. 0.5 (in fuzzy logic degree of membership terms) that the scuba tanks is filled, it means that the scuba tank is half-filled. In turn, this means that there is no risk for the diver, he/she will always be able to dive with half a tank.

The above simple example serves to illustrate a very important conceptual difference between fuzzy logic and probability. While both theories have analogies, the goal in specification of information both theories pursue is completely different. Probability determines the likelihood of occurrence of an event or condition while fuzzy logic determines the degree to which a certain event or condition is true. Further arguments detailing the advantages/disadvantages of fuzzy logic over probability theory, including a discussion on the comparison at a programmatic level can be found in [Lai 1992]. It seems clear then that both theories, while having certain aspects such as dealing with uncertainty in common, nevertheless cannot be reasoned to be identical or being contained one within the other. In fact, it seems intuitive to argue that both theories are not competitive or even exclusive but in fact complementary as argued by Zadeh in [Zadeh 1995].

In the following section, we will present the uncertainty modeling capabilities of the different types of fuzzy sets. Section (3) will highlight the different components of the interval type-2 FLC. Section (4) will present a brief overview of some of the interval type-2 FLC real world applications. Finally, Section (5) will present the conclusions and future work.

2. Uncertainty Modelling with Different Types of Fuzzy Sets.

Fuzzy Logic Systems such as fuzzy logic controllers and computing with words applications are systems based on the computation with fuzzy sets. As it is the aim of this paper to investigate the use of FLCs in such real world applications, it is essential to consider the sources of the uncertainty which we are aiming to handle and deal with using fuzzy sets of various types. While it is clear that it is hardly possible to account for all sources of uncertainty in the vast number of (potential) applications for FLCs, a series of sources of uncertainty have been well established in the literature and are widely accepted [Hagras 2007a]:

Fuzzy logic theory is based on the computation with fuzzy sets which are an extension of classical sets referred to in the context of fuzzy logic as “crisp sets”. Where in classical set theory each object can be qualified as being or not being a member of a specific set, in fuzzy logic, the membership of every object in a specific set is determined by a matter of degree referred to as “degree of membership” which is defined via a Membership Function (MF). While in type-1 fuzzy sets, the degree of membership is specified by a crisp number belonging to the interval [0, 1], in type-2 fuzzy sets, the degree of membership is in itself fuzzy and is represented by what is usually referred to as a secondary membership function. If the secondary membership function is at its maximum of 1 at every point, we speak of an interval type-2 set. Thus type-2 fuzzy sets include a third dimension and footprint of uncertainty as shown in Figure (1b) and Figure (1c) which gives them extra degrees of freedom to handle the faced uncertainties. A visual example of the three types of fuzzy sets is given in Figure (1). It should be noted that while traditionally the type-1 set is not visualised as a three-dimensional set, its conception and visualisation in three dimensions is straightforward when considering each of its points to be associated with the value 1 in the third dimension thus attaching complete confidence to each achieved membership value associated with a given crisp input.

Conceptually, type-2 fuzzy sets were introduced by Zadeh in 1975 [Zadeh 1975]. The concept’s main appeal is the notion that while type-1 fuzzy sets allow for a fuzzy representation of a term to be made, the fact that the membership function of a type-1 set is crisp means that the degrees of membership derived from the thusly specified set are completely crisp – not fuzzy. If we are very uncertain about a specific quantity, we can use type-2 sets that let us avoid a crisp membership function and result in degrees of membership which are themselves fuzzy. Of course, one can argue that even type-2 MFs are crisply defined in three dimensions and that one would require type-infinity sets to account completely for uncertainty. However this is not the case as argued by [Kreinovich 2001]. In addition, at this point in time it does not seem practical to go beyond type-2 fuzzy sets.

For now, let us focus on the three types of sets mentioned and in particular on the way they represent degrees of membership. In Figure (1), the same input p is applied to the three different types of fuzzy sets (type-1 fuzzy set in Figure (1a), interval type-2 fuzzy set in Figure (1b) and general type-2 fuzzy set in Figure (1c), resulting in a degree of membership which is specific to the type of fuzzy set. The amount of uncertainty (and the distribution) that is associated with the degree is shown in colour in Figure (1) and is explained in Figure (2). It shows the secondary Membership Functions (MFs) (third dimension) of the type-1 fuzzy set (Figure (2a)), the interval type-2 fuzzy set (Figure (2b)) and the general type-2 fuzzy set (Figure (2c)) as induced by the same input p as shown in Figure (1). It should be noted that Figure (2) is visualising the y-z plane.


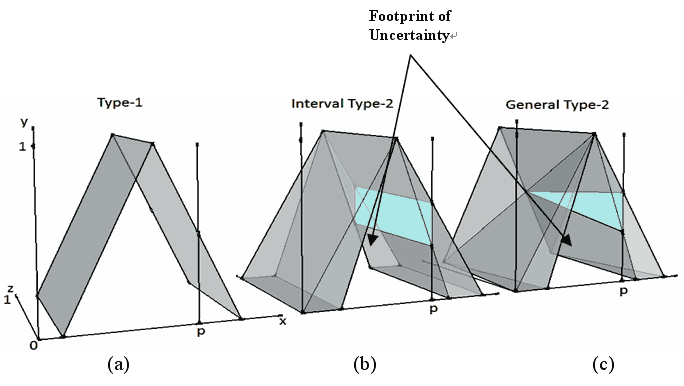
Figure (1). An example of the three types of fuzzy sets. The same input p is applied to each fuzzy set.
(a) Type-1 fuzzy set. (b) Interval type-2 fuzzy set. (c) General type-2 fuzzy set.


Figure (2). A view of the secondary membership functions (third dimensions) induced by an input p for
(a) Type-1 fuzzy set. (b) Interval Type-2 fuzzy set. and (c) General type-2 sets.

As shown in Figure (2), the secondary MF in type-1 fuzzy sets has only one value in its domain (a in Figure (2a)) corresponding to the primary membership value at which the secondary grade equals 1. Hence, in type-1 fuzzy sets, for each x value (in our case p), there is no uncertainty associated with the primary membership value [Mendel 2001]. In interval type-2 fuzzy sets as shown in Figure (2b), there is maximum uncertainty associated with the secondary membership function as the primary membership is taking values within the interval [a, b], where each point in this interval is having an associated secondary membership of 1. In general type-2 fuzzy sets as shown in Figure (2c), the uncertainty (represented by the secondary membership function) can be modelled with any degree between type-1 and interval type-2 fuzzy sets, for example by the triangular secondary membership function shown in Figure (2c). Overall, it can be noted that general type-2 fuzzy sets can model the uncertainty in the third dimension from nearly no uncertainty (i.e. type-1) to maximum (i.e. interval type-2, where the uncertainty is equally spread in the third dimension).

The vast majority of the FLCs that have been used so far were based on the traditional type-1 FLCs. However, as mentioned above, type-1 FLCs cannot fully handle or accommodate for the linguistic and numerical uncertainties associated with dynamic unstructured environments as they use precise type-1 fuzzy sets. Type-1 fuzzy sets handle the uncertainties associated with the FLC inputs and outputs by using precise and crisp membership functions that the user believes capture the uncertainties [Mendel 2001]. The linguistic and numerical uncertainties associated with real world applications make it impossible to precisely specify appropriate crisp membership functions during the design stage of the FLC. If precise type-1 membership functions are still specified in order to satisfy a certain set of environmental and operating conditions, already minor changes in these said conditions render the designed type-1 system “sub-optimal” as its membership functions do not account for the new conditions. This can cause degradation in the FLC performance which can result in poor control and inefficiency. Remedying this problem for type-1 systems can lead to significant overheads (in design time and cost) as it involves the frequently redesign or tuning of the type-1 FLC so that it can deal with the various uncertainties faced in dynamic unstructured environments.

The general type-2 FLC is computationally intensive [Liang 2000] and the computation simplifies a lot when using interval type-2 FLC (using interval type-2 fuzzy sets) which will enable us to design a FLC that operates in real time. This is why the vast majority of type-2 FLC are based on Interval Type-2 FLCs (IT2FLCs) that employ interval type-2 fuzzy sets. However, new theories are emerging which should enable the realization of general type-2 FLCs that operate in real time [Wagner 2009], [Mendel 2008], [Coupland 2007].

3. Interval Type-2 FLC

The IT2FLC is depicted in Figure (3) and it consists of a Fuzzifier, Inference Engine, Rule Base, Type-reducer and Defuzzifier.

The IT2FLC works as follows: the crisp inputs from the input sensors are first fuzzified into input interval type-2 fuzzy sets. Singleton fuzzification (where the input value is represented by precise crisp value) is usually used in interval type-2 FLC applications due to its simplicity and suitability for embedded processors and real-time applications. The input interval type-2 fuzzy sets then activate the inference engine and the rule base to produce output interval type-2 fuzzy sets. The interval type-2 FLC rules will remain the same as in Type-1 FLC (T1FLC), but the antecedents and/or the consequents will be represented by interval type-2 fuzzy sets. The inference engine combines the fired rules and gives a mapping from input interval type-2 fuzzy sets to output interval type-2 fuzzy sets. The interval type-2 fuzzy outputs of the inference engine are then processed by the type-reducer, which combines the output sets and performs a centroid calculation that leads to type-1 fuzzy sets called the type-reduced sets. In the interval type-2 FLCs used so far, there are two ways to perform type-reduction: using the iterative Karnik-Mendel (KM) procedure to calculate the type-reduced fuzzy sets or using the Wu-Mendel uncertainty bounds method to approximate the type-reduced set [Wu 2004]. After the type-reduction process, the type-reduced sets (or approximate type-reduced sets) are then defuzzified (by taking the average of the type-reduced/approximated type-reduced set) to obtain crisp outputs that are sent to the actuators. More information about the interval type-2 FLC can be found in [Hagras 2004] and the IEEE Expert Now module [Hagras 2008].

It has been argued that using interval type-2 fuzzy sets to represent the inputs and/or outputs of FLCs has many advantages when compared to type-1 fuzzy sets, some of which are:


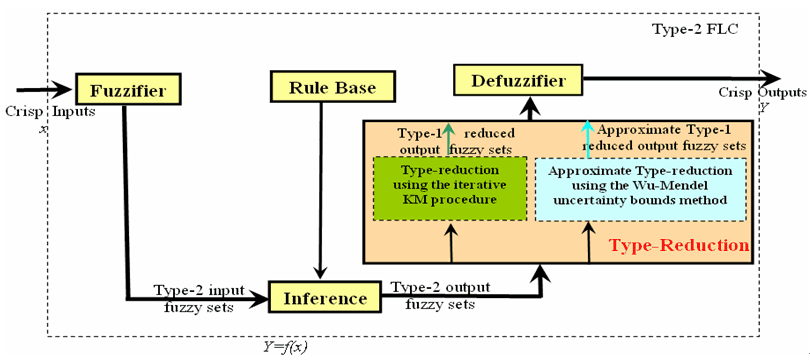
Figure (3). The interval type-2 FLC.

4. Overview on Some Interval Type-2 FLC Real World Applications

In this section, we will highlight some of the IT2FLC real world successful applications. IT2FLC have been successfully applied to the field of marine diesel engines as reported in [Lynch 2005], [Lynch 2006]. Marine diesel engines are huge engines which due to their vast sizes and large power outputs require accurate and robust speed control/governing. Accurate speed control of marine diesel engines is of critical importance as significant deviations from the speed set point could be detrimental in terms of performance and potentially damaging to the engine. Moreover, for applications such as power generation, the engine speed in rpm must be stable multiples of the generated base frequency i.e. 50Hz frequency would require the engine to operate at 1000 rpm, 1500 rpm etc. Hence, significant speed deviation can cause the generation of incorrect frequencies resulting in loss of synchronisation between the generator and associated power grid.

There are many sources of uncertainties facing the speed controller of marine diesel engine including input uncertainties (due to sensor measurements affected by high noise levels i.e. electromagnetic and radio frequency interference, vibration induced triboelectric cable charges, etc), output uncertainties (due to actuators wear and tear, etc) and most importantly uncertainties in operation and load conditions (due to varying loads, weather and sea conditions, wind strength, hull fouling, vessel displacement (dependant on cargo), etc) as well as designers varying opinions for the choice of the control parameters Due to these uncertainties the current control strategies that employ T1FLCs or PID controllers require continuous tuning to deal with the various faced uncertainties. There have been various developments of this IT2FLC which resulted in commercial embedded Type-2 Neuro FLCs (T2NFC (which employ the iterative Karnik-Mendel procedure and RT2NFC (which employs the Wu-Mendel Uncertainty Bounds method). It was noticed that the performances of the RT2NFC and the T2NFC were similar to the commercially employed Viking 25 PID controller and type-1 FLC when introducing the disturbance of 20 percent load that they were tuned to handle. However, as the uncertainty associated with the change of load increases to 100 percent load as shown in Figure (4a) and Figure (4b), the performance of both the Viking 25 and type-1 FLC degrades significantly, producing large overshoots/undershoots as well as long settling times. The performance of Viking 25 and the type-1 FLC is unacceptable under these levels of uncertainties and both controllers are not applicable to real world applications under said conditions. Thus, the common practice in such situations is to retune the controller, which is a time-consuming process. On the other hand, both the RT2NFC and the T2NFC produced IT2FLCs that handled effectively the uncertainties associated with the change of the load and operation condition to give a very good performance that has small overshoots/undershoots as well as short settling times. The performance of both the RT2NFC and the T2NFC satisfy the required standards under all conditions and thus require no further tuning. Therefore, the RT2NFC and T2NFC can be used effectively to produce accurate and robust speed controllers for marine diesel engines. This shows the potential of IT2FLCs, which, as the level of uncertainties increases, are able to better handle the uncertainties and outperform the Viking25 and type-1 fuzzy logic controllers.


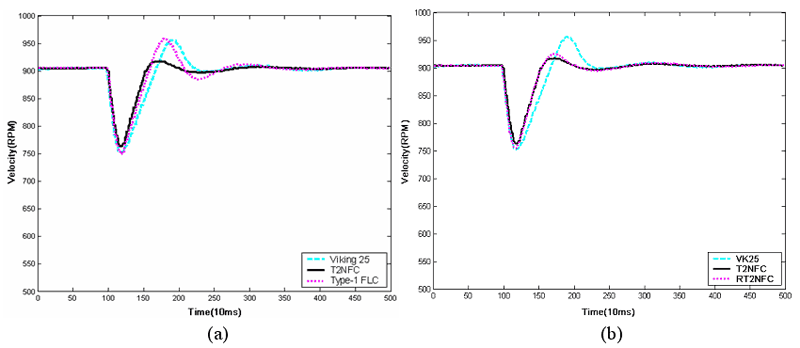
Figure 4. (a) Comparison of the response of 20 percent type-1 FLC and Viking 25 against a T2NFC with 100 percent load addition [Lynch 2006]. (b) Control response of the RT2NFC, T2NFC and Viking 25 to the uncertainties associated with load changes of 100 percent [Lynch 2006].

In [Lin 2005], an IT2FLC was applied to the control of a buck DC-DC converter. DC-DC converters are electronic systems that convert one level of electrical voltage into another level (usually) by a switching action. The DC-DC converters are used extensively in personal computers, computer peripherals, and adapters of consumer electronic devices. They are an intriguing subject from a control point of view due to their intrinsic nonlinearity. The control technique for DC-DC converters must cope with their wide input voltage and load variations to ensure stability in any operating condition while providing fast transient response. The control problem is to control the duty cycle so that the output voltage can supply a fixed voltage in the presence of the input voltage uncertainty and load variations. It has been shown that the performance of the IT2FLC is better than its type-1 counterpart where the rise time response of IT2FLC is faster than that of T1FLC with no overshoot in the IT2FLC controlled system [Lin 2005].

In [Wu 2004], a Genetic Algorithm was used to evolve an IT2FLC to control a liquid-level process. It was observed that both the type-1 and the interval type-2 FLCs are able to attenuate the oscillations when the modelling uncertainties are small. The liquid level in the tank will eventually reach the desired set-point, though the settling time is shorter when the IT2FLC is employed. When the modelling uncertainties are larger, the T1FLC will give rise to persistent oscillations while the IT2FLC has the ability to eliminate these oscillations and the liquid level reaches its desired height at a steady state. It was concluded that the IT2FLC is more robust than the T1FLC as the IT2FLC outperforms its type-1 counterpart, especially when the uncertainty is large [Wu 2004].

As in the above industrial applications, it was also noticed, for the feedback control system reported in [Sepúlveda 2005], that without uncertainties, the T1FLC and the IT2FLC responses are very similar. However, as the level of uncertainties increases, the IT2FLC produces a much improved performance with lower overshoot errors and better settling times than the type-1 counterparts. Thus, it was concluded that using an IT2FLC in real-world applications is potentially a better choice as the amount of uncertainty in real world systems is difficult to estimate [Sepúlveda 2005].

In [Zarandi 2007] an IT2FLC was presented for the desulphurization process of a real steel industry in Canada. It is shown that the proposed type-2 fuzzy logic system is superior in comparison to multiple regression and type-1 fuzzy logic systems in terms of robustness and error reduction.

IT2FLCs have several applications in the field of autonomous mobile robots. As mobile robots navigating in real-world unstructured environments must be able to operate under the conditions of imprecision and uncertainty present in such environments, IT2FLCs have found good grounds for application in mobile robot control. In [Hagras 2004], the interval type-2 FLC was applied to robot control involving indoor and outdoor robots and it was noticed that the IT2FLC always outperformed its type-1 counterpart while using a smaller number of rules. This was particularly visible through the robot paths and the control surfaces, which graphically represent the unknown function articulated by the FLC.


Figure 5. (a) The outdoor robot path using a type-2 FLC to implement the right edge following behaviour to follow an irregular edge. (b) The robot path using a type-1 FLC which gave a bad response when the environment changed (windy weather) [Hagras 2004].

In [Hagras 2004], experiments with robots in outdoor unstructured environments were presented to evaluate the real-time performance of the robot interval type-2 FLC and how it handles the large amounts of uncertainty and imprecision facing the mobile robots in such changing and dynamic environments. The robots were tested under different environmental conditions (like rain, wind, sunshine, etc.) and different ground conditions (such as slippery and dry grounds) as well as different times of the day. These experiments also involved the use of different challenging environmental features like metallic and plant edges which present additional challenges such as a bad sonar response. It has been shown that the type-2 FLC shown in Figure (5a) can better handle uncertainties to give a better response while using a smaller rule base (of 4 rules only). It was also noticed that the type-1 FLC can give a good response under specific weather, ground and robot conditions, but if any of these conditions change (e.g. operating in a windy weather condition), then the type-1 FLC with nine rules shown in Figure (5b) will give a bad response as it cannot handle the uncertainties associated with the outdoor environments.

In [Figueroa 2005], an IT2FLC was presented for a robotic agent intended to track a mobile object in the context of robot soccer games. In this domain there are many sources of uncertainty which include the image processing algorithms (which could be classified as uncertainty about the FLC inputs) as well as uncertainties in the actuators and networking resources. It was shown that the IT2FLC is able to cope with the involved uncertainty in a better way than the type-1 counterparts. It was also noted that with the IT2FLC, it is not necessary to include additional rules or fuzzy sets contrary to the T1FLC and as such, the IT2FLC uses a smaller rule base.

In [Hagras 2007b], an IT2FLC was used for the control of Ambient Intelligent Environments (AIEs). The presented agent architecture used a one-pass (non iterative) method to learn online the user’s particular behaviours and preferences for controlling the AIE in a non intrusive and seamless manner. The system learns the user behaviour by learning his particular rules and type-2 membership functions required by the type-2 fuzzy agent. These can then be adapted incrementally in a life-long learning mode to suit the changing environmental conditions and user preferences. The IT2FLC based agent was evaluated in the Essex intelligent Dormitory (iDorm). Unique experiments were conducted with various users during an extended period (spanning the course of the year) where it was possible to evaluate and demonstrate how the agent can adapt in a life-long learning mode and handle the faced short and long-term uncertainties. The IT2FLC based agents were compared to T1FLC based agents in their ability to model the user’s behaviour while handling the long-term uncertainties. The results showed that the IT2FLC was able to better model the user behaviour and handle the short and long-term uncertainties while using fewer rules.

In [Jammeh 2009] an IT2FLC was used to address the congestion control for video streaming across IP networks. In a congested network, a key problem for video is the fragile nature of the compressed stream which means that the loss of particular packets and more generally particular pictures or frames has a knock-on effect at the decoder. Video streaming is a delay-intolerant application implying that it is better to deliver a lower-quality video clip or film than to resend packets. Because of its real-time nature, measurements of available bandwidth are generally performed by observing in real-time the packet arrival statistics of the video stream packets. A network path’s available bandwidth is volatile as differing data flows including video streams arrive and leave network links along the path. This uncertainty means that equation-based congestion controllers, especially those that rely on packet loss feedback, are unsuitable. The work reported in [Jammeh 2009] has shown that the proposed IT2FLC achieved a superior delivered video quality compared to existing traditional controllers and a type-1 FLC. To show the response in different network scenarios, experiments demonstrated the response both in the presence of typical Internet cross-traffic as well as when other video streams occupied a bottleneck on an all-IP network. As All-IP networks are intended for multimedia traffic, it is important to develop a form of congestion control that can transfer to them from the mixed traffic environment of the Internet. It was found that the proposed IT2FLC though specifically designed for Internet conditions can also successfully react to the network conditions of an All-IP network. When the control inputs were subject to noise, the IT2FLC resulted in an order of magnitude performance improvement in comparison to the T1FLC. The IT2FLC also showed reduced packet loss when compared to the other controllers, again resulting in superior delivered video quality. When judged by established criteria such as TCP-friendliness and delayed feedback, fuzzy logic congestion control offers a flexible solution to network bottlenecks. Figure (6a) shows the comparisons between the type-1 and interval type-2 FLCs in terms of the packet loss percentage when increasing the noise level. An interesting and important feature of Figure (6a), is that the IT2FLC performance gracefully degrades but T1FLC performance is subject to rapid deterioration. Figure (6b) shows the comparisons between the type-1 and interval type-2 FLCs in terms of the average video quality (in dB) when increasing the noise level. It is shown that below 30% additional noise the two controllers (type-1 and interval type-2 FLCs) do not significantly deviate. However, beyond 30% of additional noise the T1FLC quality significantly degrades while the IT2FLC shows much better performance than the type-1 FLC in terms of reduced fluctuation in the sending rate and a reduced packet loss rate, both of which will be reflected in better average video quality. The IT2FLC handles the uncertainties up to high noise levels of 70% while still producing resilient performance and delivering good video quality in spite of the high noise levels faced.

As a visual comparison, the same video frame is taken from the delivered video stream after decoding and shown in Figure (7a) and Figure (7b), when the video stream was under the control of the type-1 FLC and the interval type-2 FLC respectively. The improvement from employing the IT2FLC, when there is 40% (on average) added noise, is self-evident: the T1FLC results in poor picture quality, while the IT2 FLC maintains the quality of the video in spite of the added 40% noise. These findings offer the IT2FLC as a way forward for congestion control of video streaming across packet-switched IP networks [Jammeh 2009].


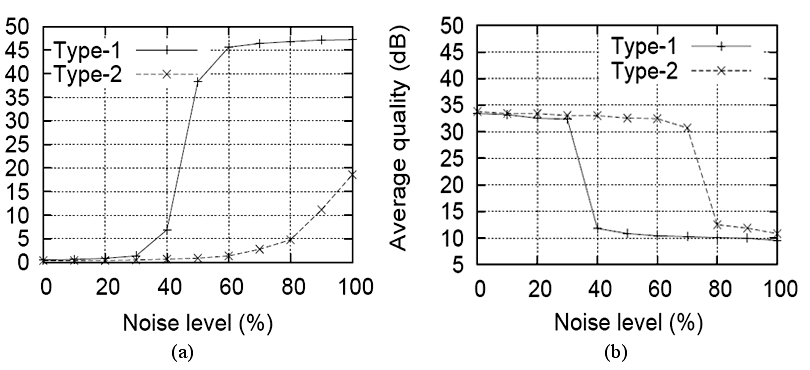
Figure 6. The performance of type-1 and interval type-2 FLC for an increasing noise level, average against (a) packet loss rate (b) video quality [Jammeh 2009].


Figure 7. Received video frame after a 40% noise level addition to delay measurements with: a) a T1 FLC, and b) an IT2 FLC [Jammeh 2009].

5. Conclusions

In this paper, we have presented the interval type-2 FLC and its components and proceeded to highlight its benefits in terms of handling large amounts of uncertainties frequently present in real world applications.

Through the review of the various interval type-2 FLC applications, it has been shown that as the level of imprecision and uncertainty increases, the interval type-2 FLC will provide a powerful paradigm to handle the high level of uncertainties present in real-world environments and applications. It has also been shown in various applications that the interval type-2 FLCs have given very good and smooth control responses that have outperformed their type-1 counterparts. Thus, using type-2 FLCs in real-world applications can be a better choice than type-1 FLCs since the amount of uncertainty in real systems most of the time is difficult to estimate.

Current research has started to explore the potential and possibility of general type-2 FLCs as in [Wagner 2009], [Mendel 2008]. This will enable to build on the existing theory of IT2FLC while exploring the power of general type-2 FLCs.

Thus with the latest developments in interval type-2 FLCs, we can see that type-2 FLCs overcome the limitations of type-1 FLCs and present a way forward to fuzzy control, especially in environments faced with a large amount of uncertainty, which includes most of the real-world applications. As such, it is envisaged to see a wide spread of type-2 FLCs in many real-world applications in the next decade.

6. References

  1. [Dubois 1993] D. Dubois and H. Prade, “Fuzzy sets and probability : Misunderstandings, bridges and gaps”, Proceedings of the second IEEE International Conference on Fuzzy Systems, Vol. 2, pp. 1059-1068, San Francisco, 1993.
  2. [Figueroa 2005] J. Figueroa, J. Posada , J. Soriano, M. Melgarejo and S. Roj, “A type-2 fuzzy logic controller for tracking mobile objects in the context of robotic soccer games,” Proceeding of the 2005 IEEE International Conference on Fuzzy Systems, pp. 359-364, Reno, USA, May 2005.
  3. [Hagras 2004] H. Hagras, “A hierarchical type-2 fuzzy logic control architecture for autonomous mobile robots,” IEEE Transactions on Fuzzy Systems, Vol.12, pp. 524-539, August 2004.
  4. [Hagras 2007] H. Hagras, “Type-2 FLCs: A new Generation of Fuzzy Controllers”, IEEE Computational Intelligence Magazine, Vol. 2, No. 1, pp. 30-43, February 2007.
  5. [Hagras 2007] H. Hagras, F. Doctor, A. Lopez, A and V. Callaghan, “An Incremental Adaptive Life Long Learning Approach for Type-2 Fuzzy Embedded Agents in Ambient Intelligent Environments,” IEEE Transactions on Fuzzy Systems, Vol. 15, No.1, pp. 41-55, February 2007.
  6. [Hagras 2008] H. Hagras, “Type-2 Fuzzy Logic Controllers: Towards a New Approach for Handling Uncertainties in Real World Environments”, IEEE Expert Now Tutorial, http://ieeexplore.ieee.org/articleSale/modulesabstract.jsp?mdnumber=EW1084 , June 2008.
  7. [Jammeh 2009] E. Jammeh, M. Fleury, C. Wagner, H. Hagras, M. Ghanbari, “Interval Type-2 Fuzzy Logic Congestion Control for Video Streaming across IP Networks”, to appear in the IEEE Transaction of Fuzzy Systems, December 2009.
  8. [Kelvin 1891] W. T. Kelvin, Popular Lectures and Addresses, Macmillan & Co. 1891.
  9. [Klir 2006] G. J. Klir, “Uncertainty and Information, Foundations of Generalized Information Theory”, Wiley, 2006.
  10. [Kreinovich 2001] V. Kreinovich, H. Nguyen, “1st Order, 2nd Order, What Next ? We Do Not Really Need Third-Order Descriptions: A View from a Realistic”, Proceedings of the International Fuzzy Systems Association Congress (IFSA 2001), pp.1908-1914, July 2001.
  11. [Liang 2000] Q. Liang, and J. Mendel, "Interval type-2 fuzzy logic systems: theory and design," IEEE Transactions on Fuzzy Systems, Vol. 8, pp. 535¬-550, October 2000.
  12. [Lynch 2005] C. Lynch, H. Hagras, and V. Callaghan, “Embedded type-2 FLC for real-time speed control of marine and traction diesel engines,” Proceeding of the 2005 IEEE International Conference on Fuzzy Systems, pp. 347 –352, Reno, USA, May 2005.
  13. [Lynch 2006] C. Lynch. H. Hagras and V. Callaghan, “Using uncertainty bounds in the design of an embedded real-time type-2 neuro-fuzzy speed Controller for marine diesel engines,” Proceeding of the 2006 IEEE International Conference on Fuzzy Systems, pp. 7217-7224, Vancouver, Canada, July 2006.
  14. [Lin 2005] P. Lin, C. Hsu and T. Lee, “Type-2 fuzzy logic controller design for buck DC-DC converters, ” Proceeding of the 2005 IEEE International Conference on Fuzzy Systems, pp. 365-2370, Reno, USA, May 2005.
  15. [Mendel 2001] J. Mendel, Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New directions, Upper Saddle River, NJ: Prentice-Hall, 2001.
  16. [Sepúlveda 2005] R. Sepúlveda, O. Castillo, P. Melin, A. Diaz and O. Montiel, “Handling Uncertainty in Controllers Using Type-2 Fuzzy Logic,” Proceeding of the 2005 IEEE International Conference on Fuzzy Systems, pp. 248-253, Reno, USA, July 2005.
  17. [Mendel 2008] J. Mendel, Feilong Liu, “On new quasi-type-2 fuzzy logic systems,” Proceedings of the IEEE International Conference of Fuzzy Systems, pp. 354-360, Hong Kong, China, June 2008.
  18. [Wagner 2009] C. Wagner and H. Hagras, “zSlices based General Type-2 FLC for the Control of Autonomous Mobile Robots in Real World Environments,“ Proceedings of the IEEE International Conference of Fuzzy Systems, Jeju Island, Korea, August 2009.
  19. [Wu 2002] H. Wu and J. Mendel, “Uncertainty bounds and their use in the design of interval type-2 fuzzy logic systems,” IEEE Transactions on Fuzzy Systems, vol.10, pp. 622-639, October 2002.
  20. [Wu 2004] D. Wu and W. Tan, “Type-2 fuzzy logic controller for the liquid-level process” Proceeding of the 2004 IEEE International Conference on Fuzzy Systems, pp. 248-253, Budapest, Hungary, July 2004.
  21. [Wu 2005] D. Wu and W. Tan, “Type-2 FLS modeling capability analysis,” Proceeding of the 2005 IEEE International Conference on Fuzzy Systems, pp. 242-247, Reno, USA, May 2005.
  22. [Zadeh 1965] L.A. Zadeh, “The Concept of a Linguistic Variable and Its Application to Approximate Reasoning-I”, Information Sciences, vol. 8, pp. 199-249, 1975.
  23. [Zadeh 1995] L.A. Zadeh, “Probability theory and fuzzy logic are complementary rather than competitive”, Technometrics, vol. 37, issue 3, pp. 271-276, August 1995.
  24. [Zarandi 2007] F. Zarandi, B. Turksen, T. Kasbi, “Type-2 Fuzzy Modeling for Desulphurization of Steel Process”, Expert Systems with Applications, Vol. 32, No. 1, 157—171, 2007.

About the Authors

Prof. Hani Hagras is a Professor in the School of Computer Science and Electronic Engineering, Director of the Computational Intelligence Centre and the Head of the Fuzzy Systems Research Group in the University of Essex, UK. His major research interests are in computational intelligence, notably type-2 fuzzy systems, fuzzy logic, neural networks, genetic algorithms, and evolutionary computation. His research interests also include ambient intelligence, pervasive computing and intelligent buildings. He is also interested in embedded agents, robotics and intelligent control. He has authored more than 150 papers in international journals, conferences and books. His work has received funding that totalled to about £2.5 Million in the last five years from the European Union, the UK Department of Trade and Industry (DTI), the UK Engineering and Physical Sciences Research Council (EPSRC), the UK Economic and Social Sciences Research Council (ESRC), the Korea- UK S&T fund as well as several industrial companies. He has also two industrial patents in the field of Computational intelligence and intelligent control. He is a Fellow of the Institution of Engineering and Technology (IET (IEE)) and a Senior Member of the Institute of Electrical and Electronics Engineers (IEEE). He is the Chair of IEEE Computational Intelligence Society (CIS) Senior Members Sub-Committee. He served as the chair of the IEEE CIS Task Force on Intelligent Agents (2007-2009) and Chair of the IEEE CIS Task Force on Extensions to Type-1 Fuzzy Sets. His research has won numerous prestigious international awards where most recently he was awarded by the IEEE Computational Intelligence Society (CIS), the Outstanding Paper Award in the IEEE Transactions on Fuzzy Systems. In addition, he was awarded the IET Knowledge Networks Award. He is an Associate Editor of the IEEE Transactions on Fuzzy Systems. He is also an Associate Editor of the International Journal of Robotics and Automation, the Journal of Cognitive Computation, the Journal of Applied Computational Intelligence and Soft Computing and the Journal of Ambient Computing and Intelligence. He served also as a guest editor in the Journal of Information Sciences and the Journal of Ubiquitous Computing and Intelligence. He is a member of the IEEE Computational Intelligence Society (CIS) Fuzzy Systems Technical Committee. He is also a member of the IEEE Industrial Electronics Society (IES) Technical Committee of the Building Automation, Control and Management. In addition he is member of the Executive Committee of the IET Robotics and Mechatronics Technical and Professional Network. Prof. Hagras chaired several international conferences where most recently he served as the General Co-Chair of the 2007 IEEE International Conference on Fuzzy systems London, July 2007 and he also served as Programme Chair for the 2008 IET International Conference on Intelligent Environments, Seattle, USA and he is currently serving as the Programme Chair of 2009 IEEE Symposium on Intelligent Agents, Nashville, USA, April 2009 and he is also a Programme Area Chair (control) for the 2009 IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, August 2009. He served as a member of the international programme committees of numerous international conferences.

Christian Wagner received his B.Sc. in Computer Science and M.Sc. in Robotics and Embedded Systems from the University of Essex, Colchester, UK. He is currently a PhD student and Senior Research Officer at the School of Computer Science and Electronic Engineering at the University of Essex, UK. Previously he has completed internships and worked in summer jobs for SES-ASTRA, GE Fanuc Automation, Sun Microsystems and Insearch Ltd. His main interests include Type-2 Fuzzy Logic, control applications, computational intelligence in general, embedded agents, robotics and pervasive computing.