Three-dimensional Fuzzy Logic System
for Modeling & Control –
special applications of type-2 fuzzy system
Han-Xiong Li
Department of Manufacturing Eng & Eng Management
City University of Hong Kong, Hong Kong
Email:
Abstract
The traditional fuzzy logic system (FLS) can only model and control the process in two-dimensional nature. Many of real-world systems are of multi-dimensional features, such as, thermal & fluid processes with spatio-temporal dynamics, biological systems or decision-making processes that contain stochastic and imprecise uncertainties. These types of systems are difficult for the traditional FLS to model and control because they require a third dimension for spatial or probabilistic information. The type-2 fuzzy set provides the possibility to develop a three-dimensional fuzzy logic system for modeling and control of these processes in three-dimensional nature.
1. Introduction
The traditional fuzzy logic system (FLS) provides a nonlinear mapping from input x to output y [1] and further improves its performance with the neural learning [2]. It can be seen as a two-dimensional temporal system in Figure 1. In reality, many of industrial processes have multi-physical dimensions or variables that need to handle. For example, the complex stochastic process requires a third dimension for stochastic information; and many industrial processes are of spatio-temporal nature, often called “distributed parameter systems (DPS)”, which require a third dimension for spatial information. The traditional fuzzy system will find its difficulty in modeling and control of these three-dimensional (3D) systems. A completely new configuration of FLS is needed for these applications.
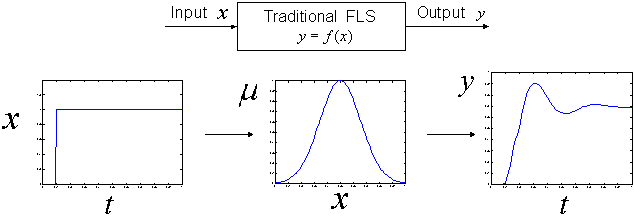
(x – input; y – output; μ - fuzzy grade; t – time)
Figure 1: Input-output mapping of a traditional FLS
A new configuration of fuzzy system, called the Type-2 FLS [3], was introduced by the end of last decade to handle the uncertainty of linguistic expression. It uses type-2 fuzzy set that was first introduced by Zadeh [4] and then studied by others [5, 6] as an extension of the ordinary fuzzy set. This type-2 fuzzy set consists of two traditional fuzzy sets, which were used by the type-2 FLS for processing uncertainties of the uncertainty. The type-2 FLS has been applied in various applications including mobile robots and environment control [7, 8]. An interval type-2 FLS was developed later to reduce its computational complexity [9, 10]. The previous development of type-2 FLS aim to improve the approximation accuracy by using two fuzzy sets for describing the same variable. If the secondary fuzzy set can be applied to other independent variables or dimensions, it will help real-world applications. Thus, a three-dimensional fuzzy logic system (3D-FLS) can be produced as shown in Figure 2 based on the concept of type-2 fuzzy system. For the easy application, the developments should follow two basic principles:
- A third dimension is created for the independent variable/dimension;
- Development should have less variations from the traditional fuzzy system;
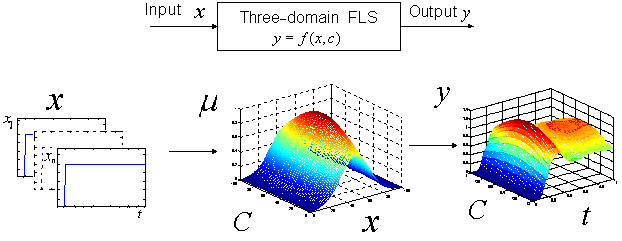
(x – input; y – output; μ - fuzzy grade; t – time; C – 3rd domain)
Figure 2: Input-output mapping of a 3D FLS
2. Probabilistic Fuzzy Logic System for Modeling
When the system becomes more and more complex, it will be more and more difficult to maintain a consistent performance due to increasing uncertainties. These uncertainties may come from various sources, such as, measurement error accumulated, unknown interactions between subsystems, and missing dynamics, etc.. In general, all these variations can be classified into two different categories as follows:
- Fuzzy uncertainty – it usually comes from the coarse measurement or imprecise perception of the process due to the harsh industrial environment.
- Stochastic variations - This is the nature of the universe. The external disturbance, insufficient sampling data, and missing dynamics, will make the situation worse.
The traditional FLS will find its difficulty in modeling of this complex process with both fuzzy and stochastic uncertainties. Recently, a probabilistic fuzzy logic system (PFLS) [11, 12] was developed, based on the concept of the type-2 FLS, by changing the secondary fuzzy MF into the probabilistic density function (PDF) for describing stochastic information of the variable. This inherent 3-dimensional (3D) system will find its application on modeling of the process with both fuzzy and stochastic uncertainties.
2.1 Configuration design
Based on the development principle described previously, the 3D-PFLS is designed to have similar functions to the traditional FLS. A potential configuration of 3D-PFLS has probabilistic fuzzification, rule base, probabilistic/fuzzy inference engine and probabilistic defuzzification, as shown in Figure 3. Different to the ordinary FLS, the PFLS uses the probabilistic fuzzy set (PFS) to express the information with stochastic uncertainties.
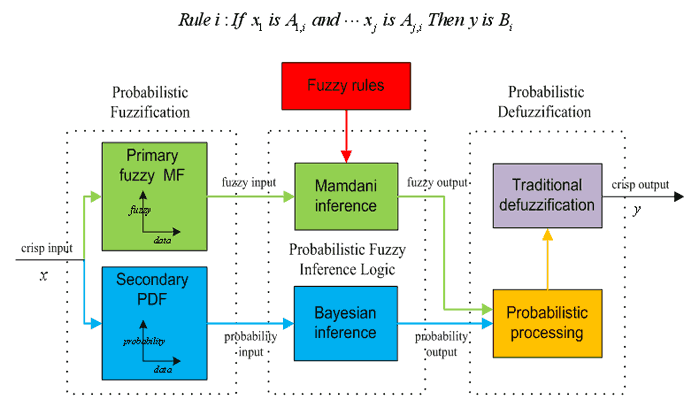
Figure 3: A Conceptual development of a 3D-PFLS
Probabilistic fuzzification
The significant difference of PFLS to FLS is that the fuzzification procedure is based on PFS instead of ordinary fuzzy sets. The primary MF will be fuzzy function and the secondary one will be designed as PDF as in Figure 4. Formation of these two will establish a 3D-MF to express both fuzzy and stochastic information. As the fuzzy and stochastic features are heavily coupled, it is not an easy work to extract the fuzzy/ stochastic features simultaneously from data, and formulate a realistic 3D-MF for most of unknown processes.
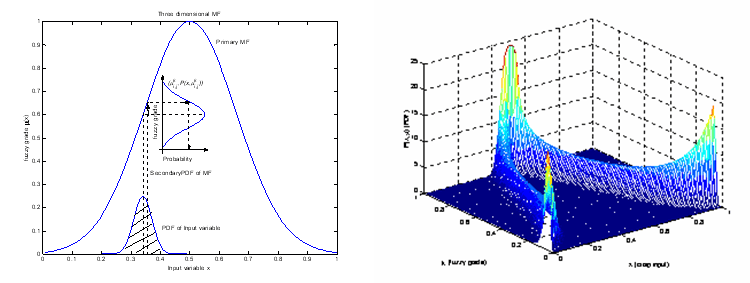
Figure 4: The three dimensional MF
Probabilistic fuzzy inference
In the earlier version of PFLS [11], the Mamdani inference engine was modified to include the probabilistic reasoning using Bayesian inference, which works well under complete dynamics. Since the secondary PDF is obtained from data learning, which always contains incomplete dynamics, the Bayesian inference may not be able to provide reliable reasoning under incomplete PDF. The most critical problem is how to integrate fuzzy reasoning and probabilistic reasoning in a more rigorous and logic way. The exponential growth of rules for multi-variables is also an important issue to address.
Probabilistic defuzzification
The existing work has integrated the expectation and centroid computation together for stochastic and fuzzy information to develop the crisp output, where the probabilistic defuzzification improves the traditional defuzzification method with the probabilistic processing method. For the decision-making system, a defuzzfication mechanism that provides a 3D output in probabilistic distribution would be useful to extract rules in probability from data.
2.2 Neural system for learning of 3D-MF
Learning from data is useful approach to compensate the uncertainty and adapt to time-varying dynamics. The neural network (NN) has the strength on learning, adaptation and parallelism. If the PFLS can be implemented in NN, it will help uncertainty learning & modeling. The Functional configuration of the neural PFLS is shown in Figure 5 to integrate fuzzy and probability processing together on the neural platform [12]. The difficulty for learning is to balance the exploration and exploitation, which will be more difficult in the stochastic environment.
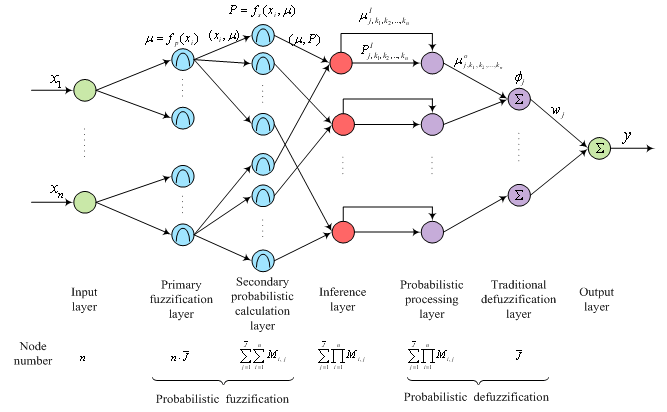
Figure 5: The structure of a neural PFLS
2.3 Application
Similar to the traditional FLS, the PFLS is capable of approximating any real continuous function on a compact set to arbitrary accuracy [12]. In the numerical example of approximating a nonlinear stochastic process in Figure 6, the neural PFLS has shown a superior modeling performance than the traditional fuzzy-neural (FNN) system, due to its inherent processing capability to both fuzzy and stochastic uncertainties.
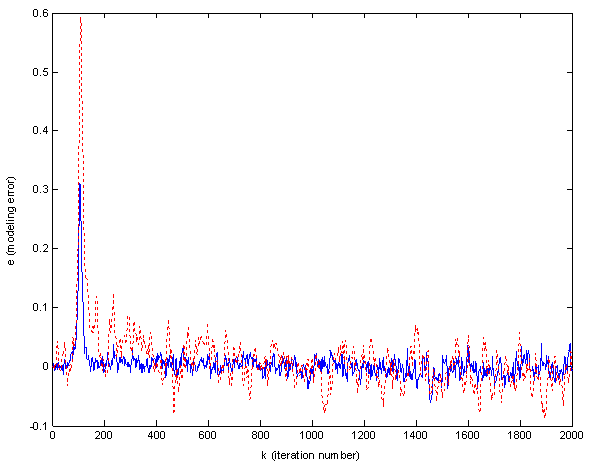
Figure 6: The performance of neural PFLS (solid blue) and FNN (dotted red)
3. Spatio-Temporal Fuzzy Logic System for Control
In the real world, many industrial processes and systems are spatio-temporal dynamic processes called DPS [13]. The distinguished features of this kind of process are that the states, controls and outputs depend on the spatial position. The DPS is traditionally controlled with model-based methods [14-16], by either ignoring the distributed nature of the process, or considering all the distributed features. In either case, a mathematical model is required.
There have been many applications of fuzzy logic control (FLC), but nearly all of them are limited to “lumped” systems, with only a few exceptional examples [17-18] that relied on assistance from other methods. This is because the tempo-spatial process has the output as a function of time and space. The traditional fuzzy system is not inherently designed for this 3D process.
3.1 Configuration design
The configuration of the FLC is designed to have the inherent ability to deal with spatial information as shown in Figure 7. Since the well developed traditional FLC provides a basic fuzzy processing platform, it is natural to combine the traditional FLC and spatial information processing. At the conceptual level, this spatio-temporal FLC has a similar functional structure to the traditional FLC which has the three basic operations of fuzzification, inference, and defuzzification. However, it will differ in the technical details because of the 3D processing requirement.
First, multiple sensors should be used to obtain the tempo-spatial information, such as a group of crisp inputs. The 3D fuzzification will transform this tempo-spatial information into 3D fuzzy inputs. Then, the 3D inference that may consist of serial operations designed for spatial information processing will produce fuzzy outputs. Finally, the defuzzification will transform fuzzy outputs into 3D output, which in practice will be a group of crisp outputs if multiple actuators are used.
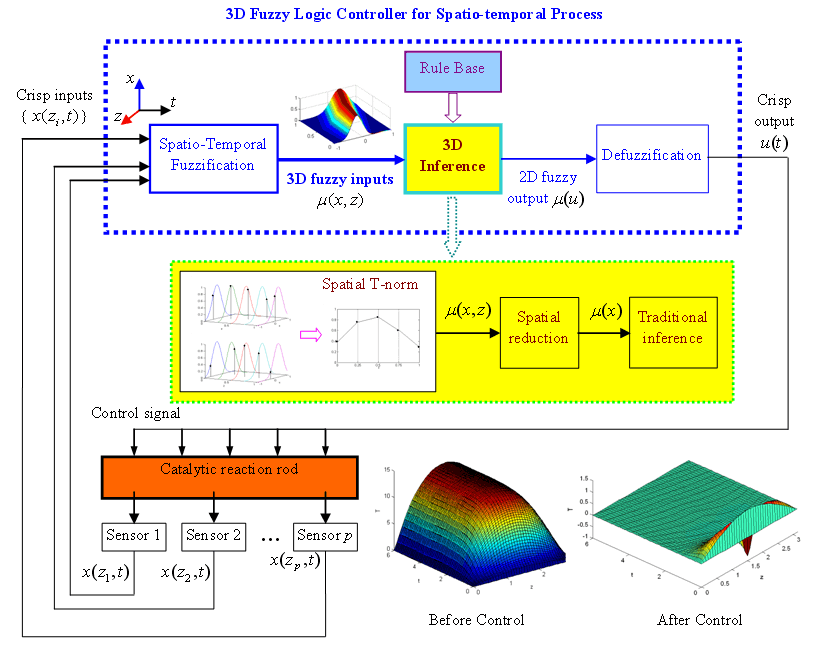
Figure 7: The configuration of spatio-temporal FLC
3D MF and fuzzification
Construction of 3D MF is a challenge in the application because it represents the tempo-spatial distribution of the process. One simple solution is to decompose it into the assembly of the 2D MF defined on each sensor input. This requires enough sensors to be located on the spatial domain. Each sensor measurement still uses the traditional 2D fuzzy set and the traditional fuzzification. A group of sensors on the space domain will provide the spatial and temporal information. Similarly, the 3D fuzzification is considered as the assembly of the traditional 2D fuzzification at each sensing location.
3D fuzzy inference logic
For 3D fuzzy set, the high-dimensional rule base is required, which will be difficult to implement in real application. An approximate and simple approach is to map the 3D fuzzy inputs onto a 2D plane, and then the traditional 2D rule inference could be applied to greatly simplify the operation. The 3D fuzzy inference logic produced has the following 3 major functions:
- Spatial T-norm
- Dimension reduction
- The traditional rule inference
The spatial T-norm is actually to fuse the spatial information from all sensing locations while doing the traditional T-norm operation for each input. The dimension reduction is to compress the 3D spatial distribution information into the 2D temporal information as described below. The centroid operation could be a good solution as it can approximately describe the overall impact of the spatial distribution. After that, the traditional 2D rule base can be used for the rule inference.

Defuzzification
After the above inference, a traditional fuzzy output is produced. Then the same defuzzification used in the traditional FLC will be taken to produce a crisp output. Like the traditional FLC, different defuzziers can be applied for different applications.
3.2 Control system design
Design philosophy
The design methodology, which is similar to the early work on the traditional FLC [19] will be proposed here for strategy design. The rule base and membership functions should be determined first by the qualitative approach, while the control structure and scaling gains should be designed quantitatively later. Similar to the traditional fuzzy-PID or PID type FLC, the control structure can be chosen as the PD structure as shown in Figure 8.
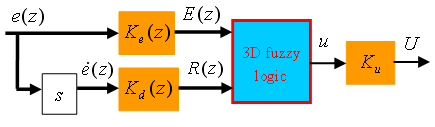
Figure 8: The PD controller structure
Rules and MF design
Knowledge base includes rules and MF. Rules can be designed very similarly to the traditional FLC because the 3D inference is developed under the framework of the 2-D inference. Therefore, a traditional linear two-dimensional rule base may still be applicable to many of the control applications. Since 3D MF is actually the assembly of 2D MF, so the traditional triangular MF can be used.
Scaling gains design
Scaling gain tuning, which directly affects the performance, requires an analytical model. The analytical approach developed by Ying [20] and modified [21] has been successfully applied to obtain the analytical model of the traditional FLC, and the even more complex FLC with the optimal reasoning [22]. If a two-dimensional linear rule base is used, and MF on each sensor input is defined as a triangle, then the previous analytical approach can also be applied here to derive a possible mathematical model. The model derived shows that PID type 3D FLC is actually a kind of sliding mode controller on the spatio-temporal domain [23].
Compared with the traditional FLC, the gain tuning of 3D FLC will be more complex. On one hand, scaling gains of 3D FLC aim to maintain control stability; on the other hand, the relative gain difference also implies the spatial distribution of the sensing inputs, and therefore will indirectly influence the shape of 3D MF. Thus, the tuning can be carried out in two hierarchical levels. At the high-level, the 3D FLC can be treated as the traditional FLC without considering the spatial influence; then the nominal value of these gains can be adjusted based on the control theory, such as the classical PID tuning [24]. At the low-level, the gain difference between different inputs from space domain should be adjusted to match the spatial distribution of the process.
3.3 Industrial application
A catalytic reaction rod is a long, thin rod in a reactor [13], as shown in Figure 7. A zero-th order exothermic catalytic reaction takes place on the rod. Since the reaction is exothermic, a cooling medium that is in contact with the rod is used to control its temperature. The long and thin rod is a typical distributed parameter system with temperature varying temporally and spatially. The rod temperature is unstable without control as shown in Figure 7. The traditional FLC will find its difficulty to stabilize the process over the whole spatial domain as shown in Figure 9. However, the proposed 3D FLC can stabilize the rod temperature easily and achieve satisfactory performance as shown in Figure 10.
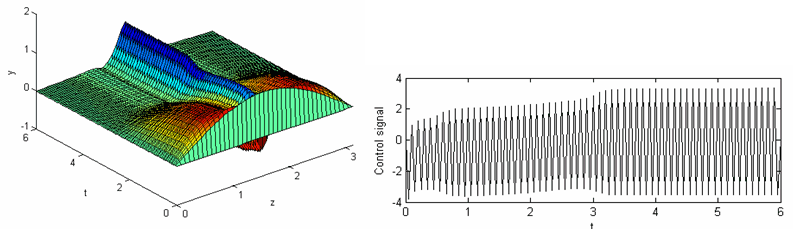
Figure 9: Unsatisfactory performance of the traditional FLC
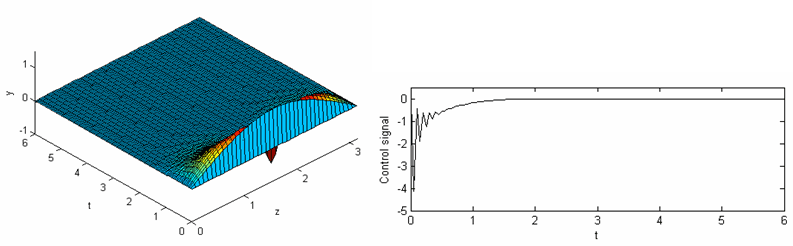
Figure 10: Satisfactory performance from 3D FLC.
4. Conclusions
The proposed 3D fuzzy systems have good potential to a wide range of real-world applications because the stochastic variation is the nature of the universe and spatio-temporal dynamics widely exist. The research is only in the beginning phase, many problems remain to study. Difficult issues include developing a realistic 3D MF from the process data, efficient generation of 3D output, and the effective way to use it, etc.. Particularly, the 3D output of PFLS will be extremely useful for the decision-making of the expert system.
Acknowledgement
The author would appreciate the contributions from Dr. Zhi Liu, Dr. Xianxia Zhang, Mr. XG Duan and Mr. Geng Zhang.
REFERENCES
1. K. Tanaka and Hua.O Wang, “Fuzzy control systems design and analysis”, Wiley, 2001.
2. Jang, J.-S.R.; Chuen-Tsai Sun; “Neuro-fuzzy modeling and control”, Proceedings of the IEEE, vol.83, 378 – 406, 1995.
3. N. N. Karnik, J. M. Mendel and Q. Liang, “Type-2 fuzzy logic systems”, IEEE Trans. on Fuzzy Systems, 7(6), 643–658, 1999.
4. L. A. Zadeh, “The concept of a linguistic variable and its application to approximate reasoning-I”, Inform. Sci., vol. 8, 199--249, 1975.
5. M. Mizumoto, K. Tanaka, “Some properties of fuzzy sets of type-2”, Inform. Contr., vol. 31, 312--340, 1976.
6. J. Nieminen, “On the algebraic structure of fuzzy sets of type-2”, Kybernetica, 13(4), 261--273, 1977.
7. H. Hagras, “A Hierarchical Type-2 Fuzzy Logic Control Architecture for Autonomous Mobile Robots”, IEEE Trans. on Fuzzy Systems, 12(4), 41-55, 2004.
8. H. Hagras, F. Doctor, V. Callaghan and A. Lopez, “An Incremental Adaptive Life Long Learning Approach for Type-2 Fuzzy Embedded Agents in Ambient Intelligent Environments”, IEEE Trans. on Fuzzy Systems, 15(1), 41-55, 2007.
9. Q. Liang and J. M. Mendel, “Interval Type-2 Fuzzy Logic Systems: Theory and Design”, IEEE Trans. on Fuzzy Systems, 8(5), 535¬-550, 2000.
10. J. M. Mendel, R. I. John and F. Liu, “Interval Type-2 Fuzzy Logic Systems Made Simple”, IEEE Trans. on Fuzzy Systems, 14(6), 808-821, 2006.
11. Z. Liu & H.X. Li, “A probabilistic fuzzy logic system for modeling and control”, IEEE Trans Fuzzy Systems, 13(6), 848 – 859, 2005.
12. H.X. Li & Zhi Liu; “A Probabilistic Neural-Fuzzy Learning System for Stochastic Modeling”, IEEE Trans. on Fuzzy Systems, 16(4), 898 – 908, 2008.
13. P. D. Christofides, “Nonlinear and Robust Control of Partial Differential Equation Systems: Methods and Applications to Transport-Reaction Processes”, Boston: Birkhäuser, 2001.
14. W. H. Ray, “Advanced process control”, New York: McGraw-Hill, 1981.
15. M. J. Balas, “The Galerkin method and feedback control of linear distributed parameter systems”, J. Math. Anal. Appl., vol. 91, 527–546, 1983.
16. R. F. Curtain, “Finite-dimensional compensator design for parabolic distributed systems with point sensors and boundary input”, IEEE Trans. Autom. Control, 27(1), 98–104, 1982.
17. J. Lin and Lewis, F.L. “Two-time scale fuzzy logic controller of flexible link robot arm”, Fuzzy Sets and Systems, 139, 125-149, 2003.
18. P. Sooraksa and Chen, G.R. “Mathematical modeling and fuzzy control of a flexible-link robot arm”, Mathl. Comput. Modeling, 27(6), 93-93, 1998.
19. H.X. Li, “Approximate model reference adaptive mechanism for nominal gain design of fuzzy control system”, IEEE Transactions on Systems, Man and Cybernetics, 29B(1), 41-46, 1999.
20. H. Ying, W. Siler & J.J. Buckley “Fuzzy Control Theory: A Nonlinear Case”, Automatica, 26(3), 513-520, 1990.
21. H.X. Li, H. Gatland & A. Green, “Fuzzy Variable Structure Control”, IEEE Transactions on Systems, Man and Cybernetics, 27B(2), 306-312, 1997.
22. H.X. Li, Zhang L, et al.“An Improved Robust Fuzzy-PID Controller with Optimal Fuzzy Reasoning”, IEEE Trans. on Syst, Man & Cyber, part-B, 35(6), 1283-1294, 2005.
23. XX Zhang, Li HX & Li SY, “Analytical Study and Stability Design of Three-Dimensional Fuzzy Logic Controller for Spatially Distributed Dynamic Systems”, IEEE Trans. on Fuzzy Systems, 16(6), 1613-1625, 2008.
24. H.X. Li & S.K. Tso, “Quantitative design and analysis of fuzzy proportional-integral-derivative control - a step towards autotuning”, International Journal of Systems Science, 31(5), 545-554, 2000.
About the Author

Han-Xiong LI (S’94-M’97-SM’00) received the the B.E. from the National University of Defence Technology, China, the M.E. degree in electrical engineering from Delft University of Technology, Delft, The Netherlands, and the Ph.D. degree in electrical engineering from the University of Auckland, Auckland, New Zealand.
Currently, he is a full Professor in the Department of Manufacturing Engineering and Engineering Management, the City University of Hong Kong. Over the last twenty years, he has had opportunities to work in different fields, including military service, industry, and academia. His research interests include intelligent control & learning, process modeling and control, and distributed parameter systems. He has authored about 90 papers in international journal with half of them in IEEE transactions.
Dr. Li serves as an Associate Editor for the IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS, PART B. He was awarded the Distinguished Young Scholar Award by the China National Science Foundation in 2004, and a “Chang Jiang Scholar” by the Ministry of Education, China in 2006.

